深入理解 Logistic Regression
在 CTR 预估领域,最基本的模型就是 Logistic Regression
本文作者深入理解LR,并总结于下。
LR 的起源
考虑二分类任务,其输出 \(y\in\{0,1\}\) ,而线性回归模型产生的预测值 \(z=w^Tx+b\) 是实数
但我们需要把 \(z\) 转换为 \(0\) 到 \(1\) 上的值,即条件概率 \(p(y=1|x)\)
最理想的是“单位阶跃函数”(unit-step function) \(y=\left\{ \begin{aligned} 0 & & z<0 \\ 0.5 & & z=0 \\ 1 & & z>0 \end{aligned} \right.\) \(0.5\) 是阈值,\(z>0\) 就是正例,\(z<0\) 就是负例
如图所示,红色那条线就是单位阶跃函数
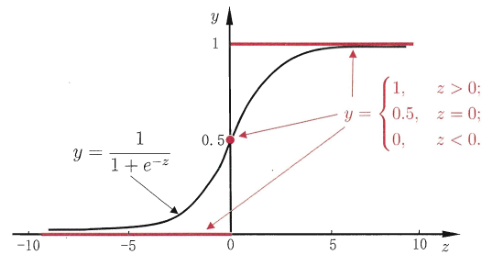
但是,单位阶跃函数不连续
由广义线性模型 \(y=g^{-1}(w^Tx+b)\) ,即 \(g(y)=w^Tx+b\)
可知,\(g(·)\) 是必须可微的,所以不连续的阶跃函数不能作为 \(g(·)\)
所以我们需要找到一个在一定程度上能近似单位阶跃函数的“替代函数”,并要求是单调可微的
符合要求的正是 logistic function: \(y=\frac{1}{1+e^{-z}}\) 上图黑色的曲线就是 logistic function,对数几率函数
对数几率函数是”Sigmoid函数”的一种代表,可以把 \(z\) 值转化为一个接近 \(0\) 或 \(1\) 的 \(y\) 值,并且其输出值在 \(z=0\) 附近变化很陡
把 logistic 函数代入 \(g^{-1}(·)\),得到 \(y=\frac{1}{1+e^{-(w^Tx+b)}}\) 即 \(ln\frac{y}{1-y}=w^Tx+b\)
把 \(y\) 视为正例的概率,\(1-y\) 视为负例的概率,两者的比值 \(\frac{y}{1-y}\) 成为 odds,表示 \(x\) 作为正例的相对可能性
对 odds 取对数 \(ln\frac{y}{1-y}=w^Tx+b\) ,得到 log odds,也叫 logit
由此可以看出,实际上是用线性回归模型的预测结果去逼近真实 \(y\) 的 log odds,因此模型就成为 logistic regression
虽然叫回归,但是却是种分类方法
优点有:
- 直接对分类可能性建模,无需事先假设数据分布,避免了假设分布不准确带来的问题
- 它不是仅仅预测出“类别”,而是直接得到近似概率的预测,对需要利用概率辅助决策时很有帮助
- logistic function 是任意阶可导的凸函数,有很好的数学性质,现有许多数值优化算法都可直接求最优解
如何求参数 w 和 b 的值?
若把 \(y\) 视为类的后验概率估计
\[p(y=1|x)\]则上面式子可重写为:
\[ln\frac{p(y=1|x)}{p(y=0|x)}=w^Tx+b\]显然有
\[p(y=1|x)=\frac{e^{w^Tx+b}}{1+e^{w^Tx+b}}\]和
\[p(y=0|x)=\frac{1}{1+e^{w^Tx+b}}\]通过极大似然估计法MLE估计 \(w\) 和 \(b\)
给定数据集 \(\{(x_i,y_i)\}_{i=1}^m\),logistic regression 模型最大化 “对数似然” log-likelihood为:
\[l(w,b)=\sum_{i=1}^mlnp(y_i|x_i;w,b)\]即令每个样本属于其真实标记的概率越大越好
为方便记录,令 \(\beta=(w;b)\),\(\hat x=(x;1)\) ,则 \(w^Tx+b\) 简写为 \(\beta\hat x\)
再令
\[p_1(\hat x;\beta)=p(y=1|\hat x;\beta)\]和
\[p_0(\hat x;\beta)=p(y=0|\hat x;\beta)=1-p_1(\hat x;\beta)\]则似然项重写为:
\[p(y_i|x_i;w,b)=y_ip_1(\hat x;\beta)+(1-y_i)p_0(\hat x;\beta)\]代回 \(l(w;b)\) 后,最大化即最小化下式:
\[l(\beta)=\sum_{i=1}^m(-y_i\beta^T\hat x_i+ln(1+e^{\beta^T\hat x_i}))\]\(l(\beta)\) 是关于 \(\beta\) 的高阶可导连续凸函数,根据凸优化理论,经典的数值优化算法如梯度下降法等都能求出最优解
\[\beta^*=\begin{equation} \mathop{\arg\min}_{\beta} \ l(\beta) \end{equation}\]